
Béla Bajnok
Hello, and welcome to my webpage!
I am a Professor of Mathematics at Gettysburg College. I love teaching! I have been fortunate to teach at a variety of institutions: an Ivy League university and an inner-city school, a large state university and a small residential liberal arts college. I am honored by the recognition I have received for my teaching, including Gettysburg College's Excellence in Teaching Award and the Crawford Award for Distinguished College or University Teaching by the Mathematical Association of America.
My research interests are centered around combinatorics and related fields, though I have publications in a variety of other subjects, including approximation theory, number theory, probability and statistics, partially ordered sets, extremal graph theory, and mathematical pedagogy. For reviews of some of my papers and books see Math Reviews or zbMath. Below I describe two areas that I am particularly interested in: spherical designs and additive combinatorics. I am also the author of two books: An Invitation to Abstract Mathematics, now in second edition by Springer, and Additive Combinatorics, published by CRC Press.
Over the years I have supervised the research of over 300 students. Many of these projects led to conference presentations and some to refereed journal publications. This article, published by the American Mathematical Society, describes our rather unusual research program.
As the Director of the American Mathematics Competitions, I oversee a series of annual competitions that starts with the participation of over 300,000 students and culminates in the International Mathematical Olympiad.
I am also on the Board of Pro Mathematica Arte, the organization that runs the Budapest Semesters in Mathematics and the Budapest Semesters in Mathematics Education programs.
Teaching

Even after so many years in higher education, teaching is the favorite part of my job. As a native of Hungary, I remain greatly influenced by the excellent education that I received there. Here are some of my guiding principles:
- inspiring an appreciation for mathematics is both desirable and possible at every level;
- the learning of skills (reading, writing, speaking, experimenting, etc.) is just as important as the learning of the subject matter;
- different students respond to different approaches, teaching styles, and assessment methods;
- all students should be supported academically and socially to provide a positive learning environment and a sense of belonging for everyone.
Spherical Designs
Imagine that we want to scatter a certain number of points on a sphere--how can we do it in the most "uniformly balanced" way? The answer might be obvious in certain cases, but far less clear in others. Consider, for example, the sphere \(S\) in \(3\)-dimensional Euclidean space, and suppose that we need to place six points on it: the most balanced configuration for the points is undoubtedly at the six vertices of a regular octahedron (for example, at the points \((\pm 1, 0, 0), (0, \pm 1, 0), (0,0,\pm 1)\) in case the sphere is centered at the origin and has radius 1).
The answer is perhaps equally clear for four, eight, twelve, or twenty points: place them so that they form a regular tetrahedron, cube, icosahedron, and dodecahedron, respectively. But how should we position five points? Or how about seven or ten or a hundred points, and how about higher dimensions? How can one do this in general?
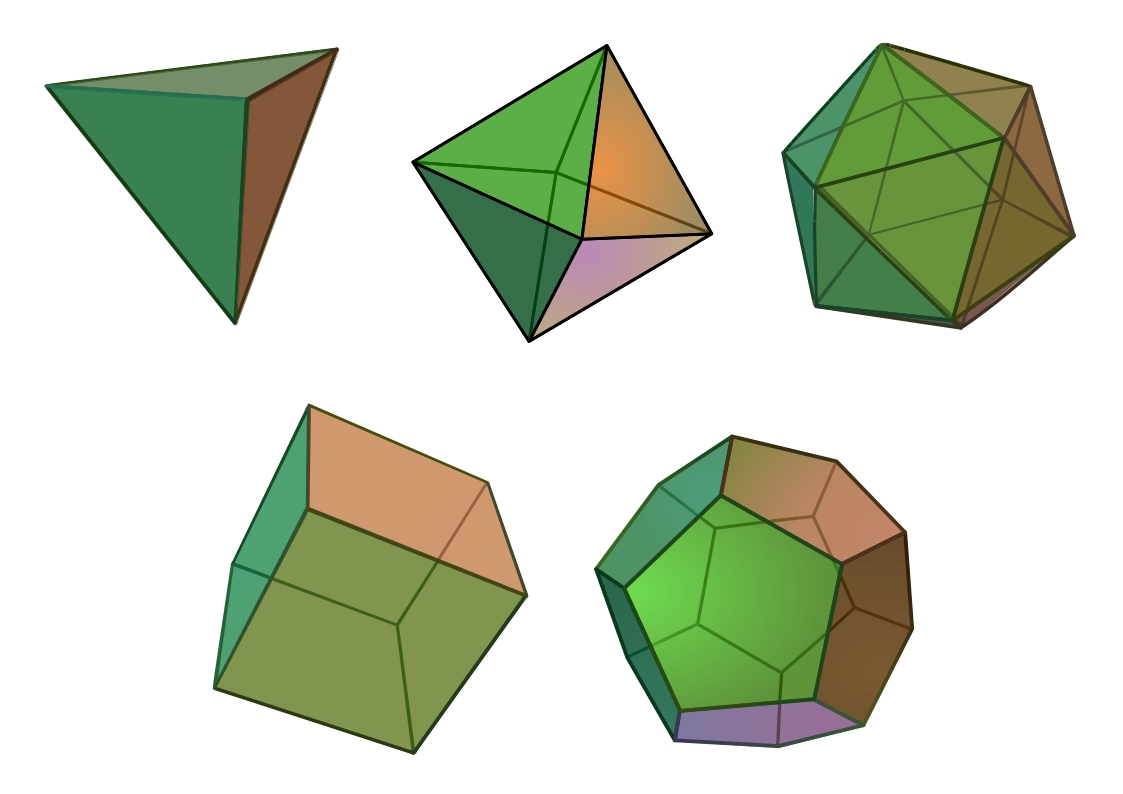
The answer to our question depends, of course, on how we measure the degree to which our pointset is balanced. For example, in the case of a packing problem, we want to place our points as far away from each other as possible; more precisely, we may want to maximize the minimum distance between any two of our points. Or, when addressing a covering problem, we want to minimize the maximum distance that any place on the sphere has from the closest point of our pointset. There are several other reasonable criteria, but the one that is perhaps the most well known and applicable is the one where we maximize the degree to which our pointset is in momentum balance: this configuration is referred to as a spherical \(t\)-design. Here \(t\) measures the degree to which the pointset is well balanced: \(t=1\) corresponds to mass balance, \(t=2\) means that the points are in both mass balance and inertia balance, and so on. A central question about spherical designs is to determine the smallest number of points that may form a spherical \(t\)-design. A version of this question was featured as "Problem 7" in Steve Smale's article Mathematical Problems for the Next Century (1999).
Additive Combinatorics
Many questions in the newly-developing yet historically-rooted area of additive combinatorics ask for "pretty" subsets in additive structures, such as abelian groups or the set of positive integers and other semigroups. There are a variety of ways to define "pretty"; here I describe only two of them, each extending the well-known and important concept of dimension in vector spaces. Consider \(G = \mathbb{Z}_{25}\), the cyclic group of twenty-five elements. A pair of complementary questions is as follows:
- What is the minimum size of a \(3\)-spanning set in \(G\); that is, a set whose elements generate all elements of the group with signed sums of at most three terms; and
- What is the maximum size of a \(3\)-independent set in \(G\); that is, a set whose elements do not generate zero with signed sums of at most three terms?
Computational tools (developed by Ivaylo Ilinkin and Peter E. Francis, respectively) for additive combinatorics calculation can be found at addcomb.gettysburg.edu.
An Invitation to Abstract Mathematics
Second Edition
Springer, 2020
View Book Site
This undergraduate textbook promotes an active transition to higher mathematics. Problem solving is the heart and soul of this book: each problem is carefully chosen to demonstrate, elucidate, or extend a concept. More than 300 exercises engage the reader in extensive arguments and creative approaches, while exploring connections between fundamental mathematical topics.
Divided into four parts, this book begins with a playful exploration of the building blocks of mathematics, such as definitions, axioms, and proofs. A study of the fundamental concepts of logic, sets, and functions follows, before focus turns to methods of proof. Having covered the core of a transition course, the author goes on to present a selection of advanced topics that offer opportunities for extension or further study. Throughout, appendices touch on historical perspectives, current trends, and open questions, showing mathematics as a vibrant and dynamic human enterprise.
This second edition has been reorganized to better reflect the layout and curriculum of standard transition courses. It also features recent developments and improved appendices. An Invitation to Abstract Mathematics is ideal for those seeking a challenging and engaging transition to advanced mathematics, and will appeal to both undergraduates majoring in mathematics, as well as non-math majors interested in exploring higher-level concepts.
Reviews of the first edition:
Bajnok’s new book truly invites students to enjoy the beauty, power, and challenge of abstract mathematics. … The book can be used as a text for traditional transition or structure courses … but since Bajnok invites all students, not just mathematics majors, to enjoy the subject, he assumes very little background knowledge. Jill Dietz, MAA Reviews
The style of writing is careful, but joyously enthusiastic…. The author’s clear attitude is that mathematics consists of problem solving, and that writing a proof falls into this category. Students of mathematics are, therefore, engaged in problem solving, and should be given problems to solve, rather than problems to imitate. The author attributes this approach to his Hungarian background … and encourages students to embrace the challenge in the same way an athlete engages in vigorous practice. John Perry, zbMATH
Additive Combinatorics: A Menu of Research Problems
CRC Press, 2018
View Book Site
Additive Combinatorics: A Menu of Research Problems is the first book of its kind to provide readers with an opportunity to actively explore the relatively new field of additive combinatorics. The author has written the book specifically for students of any background and proficiency level, from beginners to advanced researchers. It features an extensive menu of research projects that are challenging and engaging at many different levels. The questions are new and unsolved, incrementally attainable, and designed to be approachable with various methods.
The book is divided into five parts which are compared to a meal. The first part is called Ingredients and includes relevant background information about number theory, combinatorics, and group theory. The second part, Appetizers, introduces readers to the book’s main subject through samples. The third part, Sides, covers auxiliary functions that appear throughout different chapters. The book’s main course, so to speak, is Entrees: it thoroughly investigates a large variety of questions in additive combinatorics by discussing what is already known about them and what remains unsolved. These include maximum and minimum sumset size, spanning sets, critical numbers, and so on. The final part is Pudding and features numerous proofs and results, many of which have never been published.
Features:
- The first book of its kind to explore the subject
- Students of any level can use the book as the basis for research projects
- The text moves gradually through five distinct parts, which is suitable both for beginners without prerequisites and for more advanced students
- Includes extensive proofs of propositions and theorems
- Each of the introductory chapters contains numerous exercises to help readers
American Mathematics Competitions
Since 2017, I have been serving as the Director of American Mathematics Competitions (AMC).
The AMC program of the Mathematical Association of America consists of a series of competitions, curriculum materials, and engagement opportunities, designed to build problem solving skills, foster a love of mathematics, and identify talent in middle, high school, and college students across the United States.

The following competitions are open to students:
- AMC 8 Competition: for middle school students
- AMC 10 and 12 Competitions: for high school students
- Putnam Competition: for college students
Each year, over 300,000 students participate in these competitions. The best-performing high-school students may also sit for our invitational competitions, the final rounds of which are the USA Mathematical Olympiad and, for students in grade 10 and below, the USA Junior Mathematical Olympiad. We then choose about sixty students to attend the Mathematical Olympiad Program, an intensive summer institute where we continue to train the six members of the US delegation to the International Mathematical Olympiad. Our students perform extremely well at the IMO, winning the competition in four of the past five years.
Pro Mathemtica Arte
Since 2014 I have been a Board member of Pro Mathematica Arte, the organization that runs the Budapest Semesters in Mathematics and the Budapest Semesters in Mathematical Education programs. Since 2019 I am the chair of the Board’s Academic Affairs Committee.

The Budapest Semesters in Mathematics is a highly acclaimed study-abroad program for highly motivated North American undergraduate students of mathematics to experience the mathematical as well as the general culture of Hungary. Hungary boasts a tradition that combines distinction in research with the dedication to teaching and nurturing mathematical talent. Initiated by Paul Erdős, László Lovasz, and Vera T. Sós, the program provides a unique opportunity to spend a fall, spring, or summer semester in Budapest and study under the tutelage of eminent Hungarian scholar-teachers.
The Budapest Semesters in Mathematics Education program is for students interested in the learning and teaching of mathematics. Hungary has a long tradition of excellence in mathematics education. The famous Hungarian approach places emphasis on problem solving, creativity, and communication. Students learn concepts by working on problems with complexity and structure that promote perseverance and deep reflection. BSME participants immerse themselves in the Hungarian approach, observe Hungarian mathematics classrooms, and have the opportunity to plan and teach their own lessons to Hungarian students.